Light is all around us.
We need light. Plants and microorganisms harness the energy in sunlight, providing the basis for Earth's entire web of life. And, as I sit here in my yard enjoying the sunlight, I think about the first light ever created. That light still exists, it is striking the atoms of my skin right now, in the form of cosmic background microwave radiation. And I wonder, what is light, how does it work, what is its nature?
Light is the propagation of energy from one place to another. I don't just mean the light we can see. By "light" I mean all electromagnetic radiation, of which visible light is just a small part. Electromagnetic radiation is a form of energy that exhibits both wave and particle behavior at the same time. We will explore the evidence for this soon enough. Light has both electrical and magnetic field components to it as it propagates from one place to another, and these two components oscillate in phase with, and are perpendicular to, each other, and they are perpendicular to the direction that the energy is moving. This diagram shows what I mean.
This diagram represents a single unit of electromagnetic radiation, a photon. The Greek letter λ is one wavelength (frequency = 1/ λ). K represents the direction in which the photon is traveling, to the right in this case. The + and - q symbols represent positive and negative charge (q) associated with the photon. E represents the photon's energy propagating along the electrical field and B represents its energy propagating along the magnetic field. This looks complicated, but all light really is a tiny oscillation through electric and magnetic fields, carrying with it energy from one place to another.
Photons all travel at the same speed, the speed of light. The speed of light, however can be slowed when photons travel through various mediums. In a vacuum all photons travel at the same speed, c, which is 299,792,458 m/s. Photons appear to travel slower through ordinary glass, for example. The refractive index (slowing power if you will) of glass is about 1.5 so the speed of light traveling through it is c/1.5 or about 199,861,639 m/s, significantly slower. Yet this is nothing compared to how dramatically light is slowed down when it passes through a state of matter called a Bose-Einstein condensate. In 1999, researchers at Harvard University clocked light traveling through a condensate at 61 km/h! Did you notice that earlier I said "appear to travel slower"? I will explain what I mean by this later on.
Photons can pack different amounts of energy. They do this by increasing their frequency to increase their energy and vice versa.
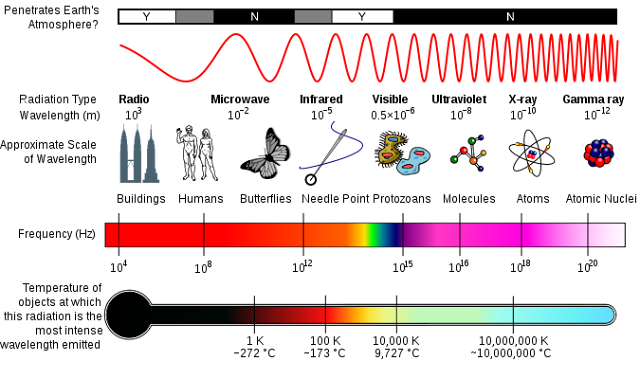
This diagram compares photons of different energies. It is what we call the electromagnetic spectrum.
Credit: Inductiveload, NASA
Look at the tiny spectrum within the frequency bar. This is visible light and these photons have frequencies between 4 x 1014 Hz (red light) and 7.9 x 1014 Hz (violet light). They are the colours of a rainbow. Violet light has more energy than red light. Gamma ray photons are of extremely high frequency and they pack the highest energy of all. These photons are released from decaying atomic nuclei when a nuclear bomb goes off or when stars explode, and they are very deadly.
How does something act like a wave and a particle at the same time? This is a great conundrum and the answer does not make sense; it comes from direct experimental evidence.
The Science of Light Started with Two Competing Theories
People have been keenly curious about light for millennia. Until the 1800's, most investigators pictured light as a beam of particles. Yet, and this is interesting, back in the 1600's, scientists such as René Descartes, Robert Hooke and Christian Huygens showed that light displayed wave behaviors such as refraction, diffraction and birefringence. However at the same time, Isaac Newton put forth his particle, or corpuscular, theory of light and he held such great sway during this century that the corpuscular theory endured for 200 years (even though he himself verged on resorting to waves to account for the interference patterns he investigated for his famous publication, Opticks). The reign of Newton ended in the early 1800's when Thomas Young and August Fresnel so clearly demonstrated light interference and diffraction that the wave model of light was finally adopted en mass. By then, James Clerk Maxwell was developing his theory of electromagnetism. Heinrich Hertz, another contemporary of this time, bridged these two theories by demonstrating that light is an electromagnetic wave, sealing the deal on the wave theory for another century. But this was not to be the final chapter on light theory . . .
Wave Theory
Let's examine the experimental evidence for the wave nature of light, as demonstrated by Young's elegant slit experiments.
When Thomas Young famously carried out this double-slit experiment in 1803 he showed that light consists of waves. It became the definitive word on light behavior and effectively shut down Isaac Newton's contemporary and competing theory that light behaved like discrete corpuscles.
He aimed a narrow beam of sunlight though an opening in a window onto a card with two slits cut into it and onto a screen placed behind on which he could see the resulting light pattern it created.
If light acts like particles he would expect the beam of light to eventually build up a pattern that corresponds to the size and shape of the slits, like what would happen if paint balls were fired over and over through two similar but larger slits in a wall. He would see something like this:
What he observed was a diffraction pattern, the beam of light passed through the narrow openings and spread out. He saw something like this instead:
Where the waves met crest to crest, constructive interference occurred, creating brighter thicker lines and where they met trough to trough, destructive interference occurred creating dimmer thinner lines.
Diffraction is what happens specifically to waves. The same results could be created with water or sound, for example.
Young performed his experiment using a beam of sunlight. He didn't have the technology to emit photons individually. In 1909, G.I. Taylor was able to reduce down his beam of light until just one photon was emitted at a time, and he got the same results as Young did a century earlier, with the appearance of interference building up with each photon that was fired.
If you are confused by this experiment, check out Dr. Quantum's animation. He describes electrons being shot off one at a time. The results are the same as for photons shot individually:
This is very strange stuff, but wait! He was shooting off individual photons one after another, so how could each subsequent photon know where to land in order to create a wave interference pattern? This result implied that photons could anticipate subsequent photons. That would have to involve some kind of communication backward through time! I will leave you to stew with this for a moment as we turn our attention to the particle nature of light.
Particle Theory
Newton's corpuscular theory of light was based on simple theoretical ideas and experiments. Subsequent and more sophisticated experiments showed very clearly that light has a distinct particle nature. Perhaps the best proof comes from the photoelectric effect. Heinrich Hertz first observed this phenomenon in the late 1880's, but it was not until the early 1900's that Albert Einstein mathematically described the photoelectric effect in terms of discrete quanta or photons. It won him the 1921 Nobel Prize in Physics. This is how the photoelectric effect works:
First of all, a photon in a light beam has a specific energy and that is determined by its frequency. If a sheet of atoms (usually a metal because metal atoms have lots of electrons around their big atoms and the electrons are bound loosely enough to be fairly easily dislodged) is struck by a single photon of sufficient energy, then an electron within the struck atom is ejected and detected on a detector. This happens because the photon's energy is absorbed by the electron and that energy is high enough to overcome the electron's binding energy, sending it flying off. If you increase the intensity of the light beam you increase the number of photons striking the metal sheet and you increase the number of electrons emitted. But you do not increase the energy each electron possesses (some of the energy absorbed by each freed electron also contributes to its increased kinetic energy as it flies off into the detector). There is a way you can increase the energy of the electrons flying off the sheet, however. You increase the frequency of the light used. Higher frequency light has more energy and more energy is transferred to the electrons. They will fly off faster because they have more kinetic energy. The photoelectric effect is explained well at the Hyperphysics site, with really good diagrams.
If light acts like waves, the electron energy would be expected to be proportional to the intensity of the light. As we see, it isn't. The electron energy depends only on the frequency (energy) of the light's photons. This concept - that a low intensity high frequency light source could dislodge many electrons and even an incredibly intense low frequency beam of light could not budge a single electron - flew in the face of well-established wave theories and was not easily accepted. None the less, Einstein managed to usher in the wave/particle theory of light, in which light manifests either its wave or particle nature according to the circumstances it finds itself in. This duality called for a new scientific paradigm, which could embrace it, and that is the concept of quantum mechanics.
Wave-Particle Duality
Quantum mechanics is the mathematical description of the wave-particle duality of matter and energy (yes, matter has this dual nature as well). It was developed in 1925 by Werner Heisenberg. In a nut-shell, it describes the time evolution of a physical system using a mathematical structure called a wave function. The wave function describes the probability that a physical system will be found in a given state at a given time. Light, in this new theoretical construct, is not a wave or a particle. It is a probability of a wave or particle at a given time. This concept describes the behavior of photons, electrons, and in fact all subatomic particle behavior. This video gives you a good idea of how the quantum mechanical model of the atom historically came about:
This is not an easily digestible idea and it might be tempting to simply leave this whole quagmire to the subatomic world where the problem of probabilities has little impact on our macroscopic world. The problem is that it does impact our everyday world. Superconductors, semiconductors, nuclear reactions and even chemical reaction mechanisms cannot be explained with classical mechanics. Cell phones, TV's and computers all rely on quantum effects. And to further convince you that quantum mechanics affects your life, consider that planets, stars, your house, and you could not exist in discrete clumps of matter if it were not for quantum mechanics at work behind the scenes inside every atom.
Quantum Electrodynamic Theory
We now have a theoretical foundation for light. Let's go further by revisiting some everyday light phenomena and testing out an even newer theoretical framework. This new framework is called Quantum Electrodynamics or QED. It describes how light and matter interact with one another using both quantum mechanics and special relativity. In fact, it is the first theory where these two concepts successfully combine and make sense. If you refer back to my unified field theory arguments in the "Universe" series of articles, you will find that the biggest challenge facing physics today is how to combine quantum mechanics with general relativity (which describes the force of gravity).
QED was first formulated in 1920 but it did not receive wide acceptance until the 1960's when, with the help of Richard Feynman and his colleagues, it was developed into the first successful quantum field theory, incorporating particle creation and annihilation into a self-consistent framework. The 1965 Nobel Prize in Physics went to them for this ground-breaking work. It has been used to precisely model such phenomena as the Lamb shift and the anomalous magnetic moment of the electron, which cannot be explained using classical physics. Late in his life, Richard Feynman gave a series of lectures on QED theory that were designed for the lay public. They are written down in the book, "QED - the strange theory of light and matter." I am drawing heavily from this book because it is the most understandable explanation of QED I have found.
Partial Reflection
I took this this photo of my desk while I'm working. In it you can see the reflection of my computer in the glass desktop. You can also see past it to the scissors in the clear plastic box under the glass. Some photons of light are reflecting from the scissors to your eyes while other photons are reflecting off the surface of the glass to your eyes. A reflection that you can see through like this is a partial reflection. The old film noir directors were experts at this kind of shot, usually through a café window.
Wave theory can explain partial reflection as interference when the light source is intense, that is, when many photons are involved, but wave theory breaks down when photons are studied individually. This is reminiscent of Taylor's refinement of Young's slit experiments.
I am going to use Feynman's example in his book to explore this phenomenon, and I urge you to pick up a copy of it for yourself.
Imagine identical red photons striking a block of clear glass straight down at a 90° angle. A device called a photomultiplier (A) is placed above the glass to catch and record any reflected photons. Another photomultiplier (B) is placed inside the glass. I know this experimental set-up is almost impossible but bear with me. This is what it looks like, with the angles altered a bit to help us see what's going on:
If the photons are directed straight down at the glass, an average of 4 photons will reflect back and arrive at detector A and 96 will arrive at detector B inside the glass. This will happen no matter how thick the glass is, as long as detector B is somewhere right below detector A. Here's the mystery with partial reflection: How can identical photons, each one shot out identically to the next, produce different results? 4% of photons decide to reflect and 96% of them decide to go through. With this simple experiment, we have just identified the probability component in quantum dynamics.
Now we will repeat the experiment by replacing the block of glass with a sheet of glass with its top and bottom surfaces exactly parallel to each other. In this case, detector A is in the same place above the glass as before but detector B is placed beneath the glass sheet. Now, photons can reflect from either the top surface or the bottom surface of the glass, so the number of reflected photons should be twice as many, around 8%, 4% of the first 100% reflecting back and 4% of the remaining 96% of photons reflecting back. Here is what the experiment like, again with the angles altered so we can see the photon paths better:
We find that this result happens with some glass sheets and not others, with the only difference between them being their thicknesses. These are our results (it doesn't matter what the real measurements are - all 3 glass sheets are very thin):
Thinnest sheet - 0% photons reflected
Medium thick sheet - 8% photons reflected
Thickest sheet - 16% photons reflected
Now we continue to use thicker and thicker sheets of glass. The amount of reflection does not continue to increase but goes down again gradually to 0%. As we continue to use thicker sheets, the cycle repeats itself. Again, over and over, if the layer of glass is one of many right thicknesses, zero reflection results.
Our prediction of 8% actually turns out to be the correct average result.
How can glass reflect 4% of the light until a back surface is added, and all of the sudden the amount of photons reflected varies from 0% to 16%? How did the photons decide to reflect in differing percentages based on where the back surface was placed, when the reflecting photons themselves never arrive at it?
No one knows how photons decide to reflect or not. But we can use QED, and specifically Richard Feynman's famous diagrams, to calculate the probability of whether a photon will reflect or go through. These diagrams are a way of calculating the probability amplitude of an event happening or not. I will show you some examples of them shortly.
Partial reflection explains why a film of diesel fuel over water is iridescent.
(Credit: John, Wikipedia)
The cycle of 0 to 16% reflection by 2 surfaces repeats more quickly if you increase the frequency of the light, so violet light reflection repeats faster than red light, for example. As a result, some thicknesses might strongly reflect both violet and red, where both of their probability amplitude crests happen to coincide, and at other thicknesses, neither may be reflected at all. The thickness of the diesel film shown above varies minutely, so you see all kinds of colours reflected back to you (this happens because sunlight is almost white light; it is composed of a mixture of frequencies: red, yellow, green and blue light - if you decided to come back at night and view the fuel slick under the light of an old-fashioned sodium street light that shines pure yellow light, you would get only yellow reflections).
Reflection from a Mirror
The established rule for calculating where light will go in this case is the angle of incidence equals the angle of reflection. This might lead you to assume that all the incident photons of light travel in one path to the mirror surface and back up again to a detector. After all, 100% of light is reflected is it not? To test this assumption, we will set up an incident light source, again red photons so they're all the same energy, at an angle of 45° to a strip of mirror and we'll place a detector where the expected path of reflected photons should reach. As you visualize the mirror you might think that the two ends of it, far from where any photons are expected to strike, will have nothing to due with the reflection. But quantum theory has something to say about that assumption. It tells you that a photon has an equal probability of striking the mirror at any point along its length, not just where the point of reflection is. In reality, the incident light does not all travel in one straight beam; it spreads out. If you use Feynman's arrows, you can draw a series of arrows, each representing the probability of a photon striking a specific point along the mirror, each of equal length (equal probability!). Each arrow will point a different direction, however. The arrows turn, like tiny stopwatches, as the photon travels, marking off how long it takes to get from source to mirror and from mirror to detector. All the arrows are then added up head-to-tail like vectors, so that opposite-directed arrows cancel each other out and those going the same direction add together. This calculation gives you, in essence a final arrow of highest probability and that arrow (did you guess it?) corresponds to the classical path of the light you predicted. Because the probability arrows differ only in the time taken by each photon, this final arrow also represents the shortest and, therefore, quickest path the photons can take. You might, very understandably, think that all I have shown you is some fancy trick that comes up with the right answer, that it doesn't prove that reflection is actually going on all over the length of the mirror.
Let's test your argument and the validity of quantum theory.
Let's chop off the mirror leaving one quarter of its length, over to the left. When we add up all the photon arrows now, we get arrows canceling each other out (the vectors actually go in a circle). We don't get any reflection. But this is what you expected of course!
Now let's take this shortened up mirror and scrape away the sections of it where arrows have a bias in one direction. For example, we add up all the arrows that point to the right, more or less. Now we have a substantial final arrow, and a strong reflection! You take a mirror that won't reflect, scrape off strips of it and, voila, it reflects. What we've done here is create a diffraction grating tailor-made for red light. Violet light has a higher frequency (the little stopwatch goes around faster) so we would have to make the strips closer together (or adjust the location of the detector). This experiment proves that light was indeed reflecting along the whole length of the mirror in the reflection experiment. You just didn't see it in that case because it all cancelled out. You can observe diffraction grating for yourself by looking at a CD at an angle.
The tiny grooves in the surface act like mirrors that are scratched in just the right places.
This technique, using Feynman diagrams, can be applied successfully to explain all light phenomena.
If you think about the mirror experiment above, you will see that light in that case was not just traveling in a perfectly straight line. Vector arrows that weren't perfectly aligned still contributed a vector component to the classically correct direction. Light reflecting just to the left and just to the right of the point of reflection significantly contributed to the final arrow of probability. This means that a beam of light does not travel in a perfectly straight line, but rather some of the light travels in a small core of nearby space. Light "smells out the neighbouring paths around it," to use Feynman's phrase in his book. If we took our mirror now and chopped off each side of it, leaving a piece that is too small for this core of light to strike it, we would not get any reflection at all. Light would then be scattered in all directions.
Here is the main point I hope to leave with you: The behavior of light in classical optics reflects not the actual photon's path but the path of greatest probability (and we can fairly accurately call this path the quickest path).
Photons and Electrons Dance Together
When we explored reflection I gave you the impression that photons bounced off the surface of the glass. Photons don't really do this. Instead they interact with electrons in the atoms that make up the glass. This interaction between photons and electrons is the basis of one of the four fundamental forces, called electromagnetism. This force is behind many phenomena we see every day, including all of chemistry and biology. All of these interactions between photons and electrons boil down to 3 basic actions:
a) A photon goes from place to place (this is not quite correct is it? I mean the probability of a photon goes from place to place!).
b) An electron's probability also goes from place to place.
c) And, finally, an electron emits or absorbs a photon.
Each of these actions has a probability amplitude (a final arrow length if you will).
A Closer Look at Refraction
Remember when I was talking about refraction as the appearance of light slowing down? The slowing is actually extra turning of the imaginary stopwatch as photons strike more electrons more often in materials that are dense in outer valence electrons (these are electrons within the atom's outermost orbital. They are more freely available to interact with photons). The photons appear to take longer to travel through such materials because they are busier being absorbed by electrons, which then emit new photons. As this goes on, the travel time for light inside the material grows longer. Bose-Einstein condensates consist of extremely tightly packed, cold and sluggish atoms, extremely dense with electrons, and that is why light takes so long to make some headway through it, as demonstrated here (with some awesome implications of the phenomenon!) in this cool video:
There is an important distinction to keep in mind here: When light is refracted, it appears to slow down, and in classical terms it does. But the individual photons involved in refraction do not slow down. In between electron emission and capture, they are motoring along at light speed. Or are they?
Electrons and photons (and again I should be more correct by calling them wave functions to remind us of their inherent uncertainty) travel a bit differently than we think of travel. They travel in space-time. Yes, this implies that they can (and do!) travel forward and backward through time. Give yourself a moment to digest that. Now, we assume that photons of light all travel at exactly the speed of light. There is a strict rule in physics that says nothing can travel faster than light speed. Well, that isn't entirely correct. Light speed, like everything else in the quantum world, has a probability. A photon can travel faster or slower than light speed, c. I assure you that at any distance appreciably longer than the diameter of an atom, all the possibilities of c cancel each other out and c is very accurately 299,792, 458 m/s. But over the tiny distances that electrons travel within an atom, this built-in variability becomes significant and must be taken into account.
Photons Live In Spacetime
To explore this idea, I will again work with an example I am borrowing straight from Feynman's book.
This is a diagram of a photon going into an electron and a (new) photon coming out, three of countless similar interactions that occur within the mirror when light strikes it. For ease, the three dimensions of space are condensed down and treated like one, so we have a time versus distance graph. The electron's movement is shown by the black arrows and the movement of the two photons involved is shown by the red arrows (these red arrows are conventionally drawn as squiggly lines but I don't have the Photoshop ability to make those). These are just three of countless possible ways this interaction could play out. And in each of these cases, where an electron absorbs a photon, continues on for a bit and then emits a photon, what we see in the everyday world is not a reflection but the scattering of light off the mirror (except in the very unlikely event that the trajectories of the two photons perfectly line up along the three spatial dimensions).
Let's take a closer look at possibility c in the diagram above because it is especially interesting. Here I have redrawn it in just a bit more detail.
I've marked out a timescale going from zero to 10 arbitrary and extremely tiny units, all positive values because we, in our everyday world, can only look at time going forward when we investigate things. From T0 to T4 we see an electron and a photon moving toward each other. At T4 something very weird happens: The photon (bottom left) suddenly disappears and two new particles appear in its place - an electron and a new particle called a positron. The important thing to remember for our purposes here is that a positron is an electron moving backward through time. Here, from our viewpoint, it appears to move towards itself. At T5 the positron and the original electron annihilate themselves and a new photon is produced. The electron created by the earlier photon continues forward in space-time.
This simple (well, not so simple) event sounds like total science fiction but it has been documented in the lab. And remember: This is just one of countless photon-electron interactions that occur every time ordinary light strikes a mirror (or any surface) and scatters. Particles are moving backwards through time right under your nose right now.
Why QED is Important
Feynman goes on to explain how photon exchanges between electrons and protons inside atoms account for how atoms of different elements exhibit different properties, a branch of science called solid-state physics, as well as how magnetism works, and how and why subatomic particles have specific spins. Finally he provides a good introduction to quantum chromodynamics, the science of how subatomic particles called quarks (these make up protons and neutrons inside the nuclei of atoms) get their spins, colours and flavours (physicists dropped the ball here with the naming). QED is an elegant theory with experimental verification to back it up. It is a powerful tool that physicists now have at their disposal and it is a major component of the Standard Model in physics.
The ultimate goal of the Standard Model is nothing short of a complete theory of all fundamental interactions, in other words, a theory of everything. The Standard Model is an example of Quantum Field Theory where each field describes, or is mediated by, a fundamental particle (photons and electrons are fundamental particles). It's not complete. Physicists are still looking for the particle that mediates gravity fields, called the hypothetical graviton, and the Higgs boson, the particle that is believed to give objects mass. Dark energy is not accounted for yet either, all of which are central to the physics of general relativity. The discovery of the Higgs boson alone would be instrumental in bridging the gap between relativity and quantum theory.
A Universe Without Electromagnetic Radiation (Without Light)?
You and everything else are made up of atoms. Within each atom, electrons orbit (within probability clouds called orbitals) around a nucleus made up of protons and neutrons. Each electron is held within a certain range away from the nucleus by photon exchanges between it and a proton. If it were not for these photon exchanges and the fact that electrons are polarized (another phenomenon that can be explained using QED theory), all atoms would have the same properties and electrons would all cluster together near their nucleus. They would not be easily attracted to other atoms, so all chemical and biological reactions would be impossible. Not only that, but all matter in the universe would behave something like, but different from, smeared out neutron star matter. Physicists think that inside neutron stars neutron degenerate matter exists, where electrons under great pressure collapse into the nucleus and merge with protons to form neutrons. Would matter even exist in a universe without electromagnetism? Almost all the elementary particles that mediate the fundamental forces have electrical charges and magnetic moments. There would be no magnetic or electrical forces. Stars, even if they could exist in some neutron star-like form, could not emit energy. A universe without light (electromagnetic force) would be absolutely unrecognizable, and unlivable, to us!
Electromagnetic energy is being propagated by photons and exchanged by electrons inside every atom of you right now. You could say, with some accuracy, that you are infused with light. The warmth you feel and all the processes of life your tissues and cells are busy with, and just about everything going on around you this moment is taking place because energy is being transferred place to place by photons.











No comments:
Post a Comment
Note: Only a member of this blog may post a comment.